数组
大约 5 分钟
566. 重塑矩阵 (简单题)
在 MATLAB 中,有一个非常有用的函数 reshape ,它可以将一个 m x n 矩阵重塑为另一个大小不同(r x c)的新矩阵,但保留其原始数据。 给你一个由二维数组 mat 表示的 m x n 矩阵,以及两个正整数 r 和 c ,分别表示想要的重构的矩阵的行数和列数。重构后的矩阵需要将原始 矩阵的所有元素以相同的 行遍历顺序 填充。如果具有给定参数的 reshape 操作是可行且合理的,则输出新的重塑矩阵;否则,输出原始矩阵。
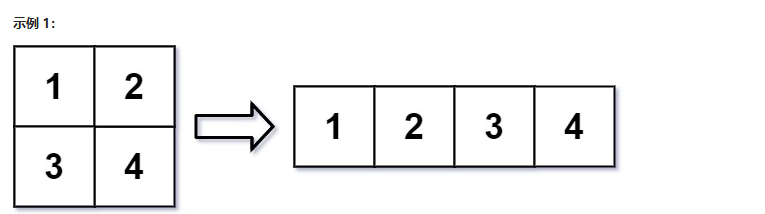
输入:mat = [[1,2],[3,4]], r = 1, c = 4
输出:[[1,2,3,4]]
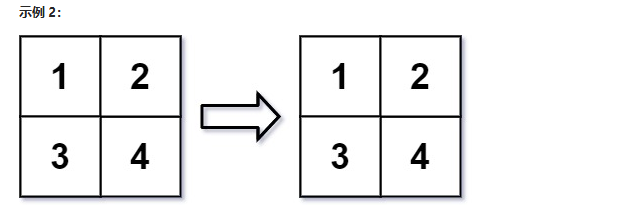
输入:mat = [[1,2],[3,4]], r = 2, c = 4
输出:[[1,2],[3,4]]
题解:
class Solution {
public:
vector<vector<int>> matrixReshape(vector<vector<int>>& mat, int r, int c) {
int m = mat.size();
int n = mat[0].size();
if (m * n != r * c)
return mat; //判断是否符合
vector<vector<int>> res(r, vector<int>(c));
for (int i = 0; i < m * n; i++)
res[i/c][i%c] = mat[i/n][i%n]; //一次遍历 把符合的都放入
return res;
}
};
118. 杨辉三角(简单题)
给定一个非负整数 *numRows,*生成「杨辉三角」的前 numRows 行。
在「杨辉三角」中,每个数是它左上方和右上方的数的和。
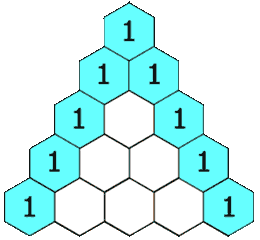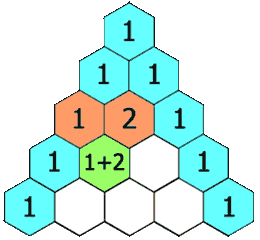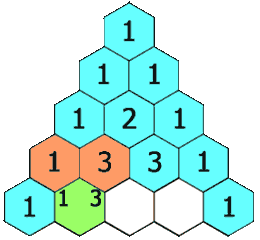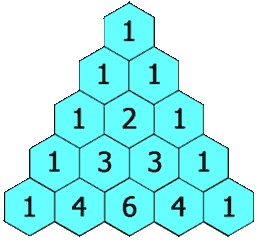
输入: numRows = 5
输出: [[1],[1,1],[1,2,1],[1,3,3,1],[1,4,6,4,1]]
输入: numRows = 1
输出: [[1]]
题解:
class Solution {
public:
vector<vector<int>> generate(int numRows) {
vector<vector<int>> res(numRows);
for (int i = 0; i < numRows; i++)
{
res[i].resize(i + 1);
res[i][0] = 1;
res[i][i] = 1;
for (int j = 1; j < i; j++)
res[i][j] = res[i - 1][j - 1] + res[i - 1][j]; //规律 在此
}
return res;
}
};
36.有效的数独(中等题)
请你判断一个 9 x 9 的数独是否有效。只需要 根据以下规则 ,验证已经填入的数字是否有效即可。
数字 1-9 在每一行只能出现一次。 数字 1-9 在每一列只能出现一次。 数字 1-9 在每一个以粗实线分隔的 3x3 宫内只能出现一次。(请参考示例图)
注意:
一个有效的数独(部分已被填充)不一定是可解的。 只需要根据以上规则,验证已经填入的数字是否有效即可。 空白格用 '.' 表示。

输入:board =
[["5","3",".",".","7",".",".",".","."]
,["6",".",".","1","9","5",".",".","."]
,[".","9","8",".",".",".",".","6","."]
,["8",".",".",".","6",".",".",".","3"]
,["4",".",".","8",".","3",".",".","1"]
,["7",".",".",".","2",".",".",".","6"]
,[".","6",".",".",".",".","2","8","."]
,[".",".",".","4","1","9",".",".","5"]
,[".",".",".",".","8",".",".","7","9"]]
输出:true
输入:board =
[["8","3",".",".","7",".",".",".","."]
,["6",".",".","1","9","5",".",".","."]
,[".","9","8",".",".",".",".","6","."]
,["8",".",".",".","6",".",".",".","3"]
,["4",".",".","8",".","3",".",".","1"]
,["7",".",".",".","2",".",".",".","6"]
,[".","6",".",".",".",".","2","8","."]
,[".",".",".","4","1","9",".",".","5"]
,[".",".",".",".","8",".",".","7","9"]]
输出:false
解释:除了第一行的第一个数字从 5 改为 8 以外,空格内其他数字均与 示例1 相同。 但由于位于左上角的 3x3 宫内有两个 8 存在, 因此这个数独是无效的。
题解:
class Solution {
public:
bool isValidSudoku(vector<vector<char>>& board) {
int row[9][9] = {0}; //建立行的哈希表
int col[9][9] = {0}; //建立列的哈希表
int tmp[3][3][9] = {0}; //建立 3 × 3 的哈希表
for (int i = 0; i < board.size(); i++)
{
for (int j = 0; j < board[0].size(); j++)
{
if (board[i][j] != '.')
{
int index = board[i][j] - '0' - 1; // -1 是因为下标的原因
row[i][index]++;
col[j][index]++;
tmp[i/3][j/3][index]++; //并且九宫格内次数也要+1,例如也是第1行第一列,i/3 j/3会自动定位到所在的小宫格
if (row[i][index] > 1 || col[j][index] > 1 || tmp[i/3][j/3][index] > 1)
return false;
}
}
}
return true;
}
};
73.矩阵置零(简单题)
给定一个 *m* x *n* 的矩阵,如果一个元素为 0 ,则将其所在行和列的所有元素都设为 0 。请使用 原地 算法**。**
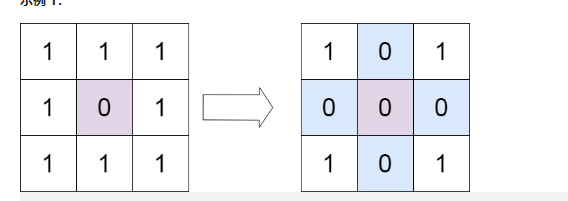
输入:matrix = [[1,1,1],[1,0,1],[1,1,1]]
输出:[[1,0,1],[0,0,0],[1,0,1]]
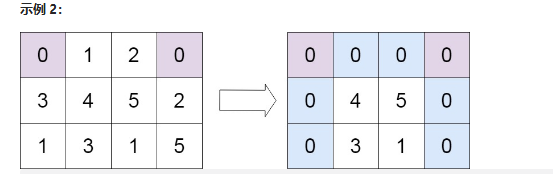
输入:matrix = [[0,1,2,0],[3,4,5,2],[1,3,1,5]]
输出:[[0,0,0,0],[0,4,5,0],[0,3,1,0]]
题解:
class Solution {
public:
void setZeroes(vector<vector<int>>& matrix) {
vector<bool> row(matrix.size());
vector<bool> col(matrix[0].size());
for (int i = 0; i < row.size(); i++)
{
for (int j = 0; j < col.size(); j++)
{
if (!matrix[i][j])
{
row[i] = true;
col[j] = true;
}
}
}
for (int i = 0; i < row.size(); i++)
{
for (int j = 0; j < col.size(); j++)
{
if (row[i] || col[j])
matrix[i][j] = 0;
}
}
}
};